数据结构 | 哈希表 Hash Table | UntitledPenguin Factory—

[最后更新于 2024-05-18]

属性

哈希表是一种基于key-value来存储和检索数据的方法使得每个数据在常数时间复杂度就可以完成查找和插入操作。

我经常把这种操作想象成幼儿园的小朋友和他们的抽屉的例子:在普通的列表里，一个小朋友想查询自己的物品，在不知道谁的抽屉是谁的情况下只能通过依次打开这100个抽屉来找到自己的物品。

但是在哈希抽屉里，每个小朋友都通过一个编号和抽屉做了对应，而每个小朋友都可以通过简单的计算直接直到自己抽屉的编码于是找到自己的东西。比如说，通过小朋友的生日/学号/姓氏简写字母来对应抽屉的号码。这样就可以快速查询自己的抽屉。

当然，我们知道这些都会产生“冲突”的情况，比如说两个小朋友同年同月同日生他们又不愿意共用抽屉。那么哈希表的设计还需要帮助他们解决冲突。

于是，这个故事已经引出了设计一个优质好用的哈希表所需要的关键组件：

关键组件

哈希函数：

一个将key-value转换为整数（Hash Code）的函数。也就是上述内容中，将每个小朋友对应到一个抽屉编号的函数。一个优质的哈希函数能够尽量的避免这种一个函数

哈希桶（Hash Bucket）：

一个使用哈希函数生成的hash code用作索引的数组。也就是我们说的带标签的抽屉（只要能够通过关键值来识别，内部又包含着所需要查询的信息，是抽屉还是桶其实本质上都差不多啦）。

解决哈希冲突：

用于处理多个关键值检索到相同索引的情况的解决办法——两个小朋友在当前的哈希函数产生的索引值需要他们“共用抽屉”。常见的方法包括链表法（chaining）和开放地址（open addressing）法，之后还会逐一介绍。

通过构造这样的哈希表，在我们查询某个关键值（key）时，只需要查询 $a[f(key)]$ ，就可以检索到该关键值的相关信息。比如下图，我们通过将姓名转换为简写的字符串然后对11取模（此处数据量不大固选了11举例）会得到一个常数，然后用该常数作为索引值就可以快速查询到该姓名所在的位置从而调取相关数据：

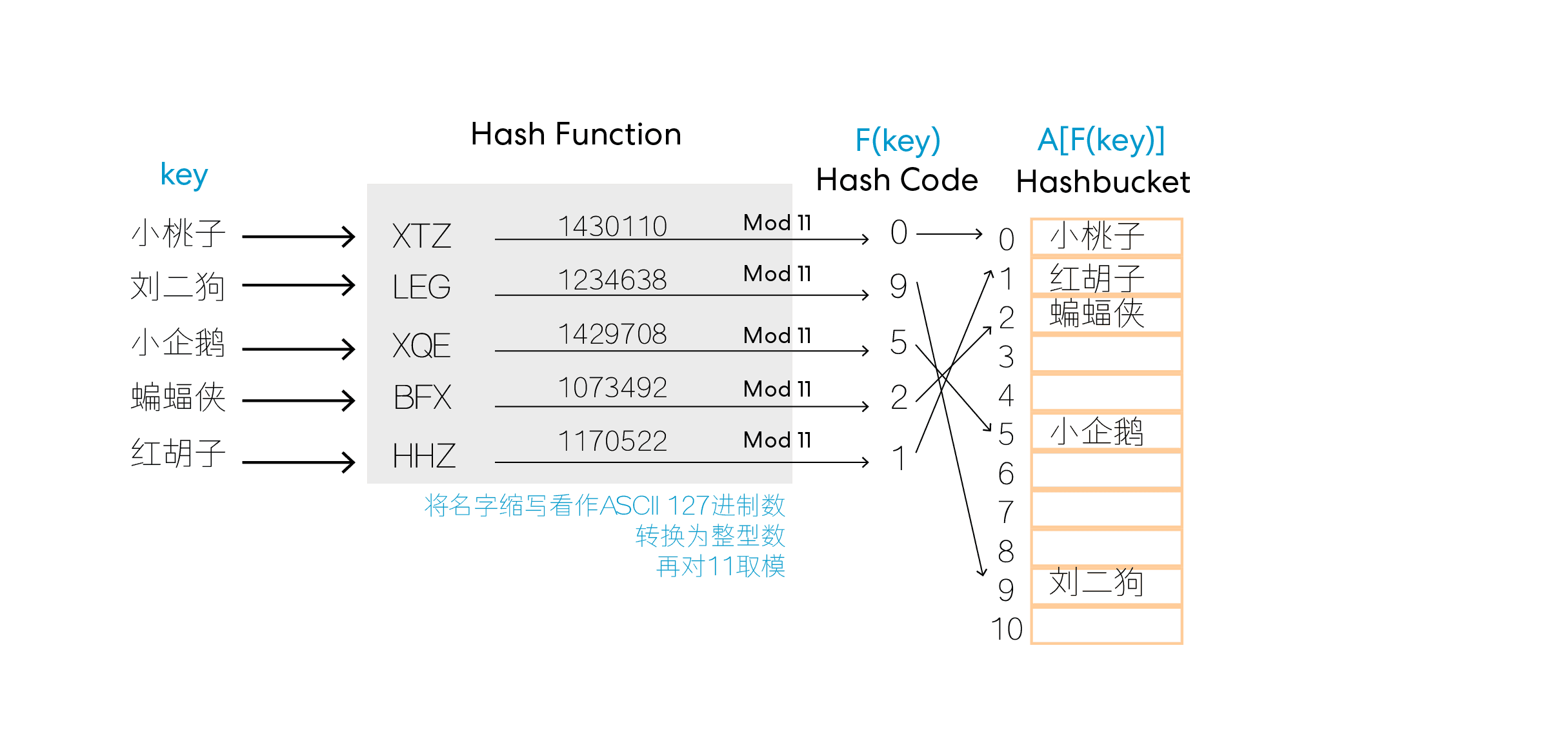
解决哈希冲突的方式

刚刚也提到了，既然用这种方法，我们自然而然就会想到，如果出现两个值冲突怎么办，较为常见的有如下两种方法。

1. 在冲突处构造链表（Chaining）

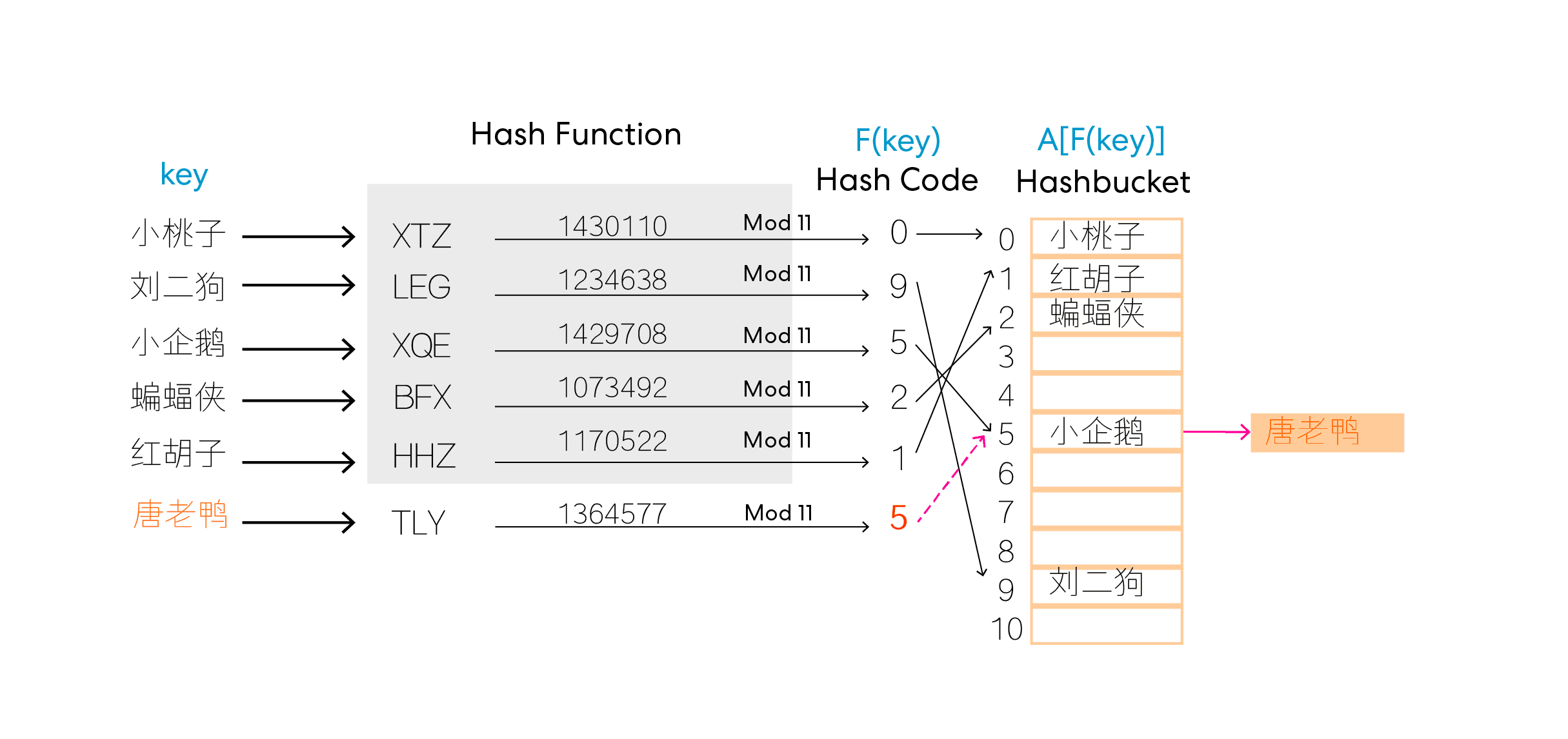
最简单的方法就是在冲突的地址构造一个链表来解决问题，比如说，新的数据“唐老鸭”和已有的词条“小企鹅”通过哈希函数返回值都是5，那么我们就在5处构造链表，也就是5处不再只有一个值，相当于变成了一个list。在查询时，只需要遍历5处链表里的所有值即可，插入与删除操作也相对于开放地址法更加简单灵活。但是，由于哈希表本身希望查询时间快速高效，这样的链表当然不能太长，否则甚至有退化为O（n）的风险（最坏情况下所有元素都冲突了），而且存放指针也占用了额外的存储空间。因而，最重要的还是要设计高效的哈希函数来解决问题。

2. 开放地址法（Open Addressing）

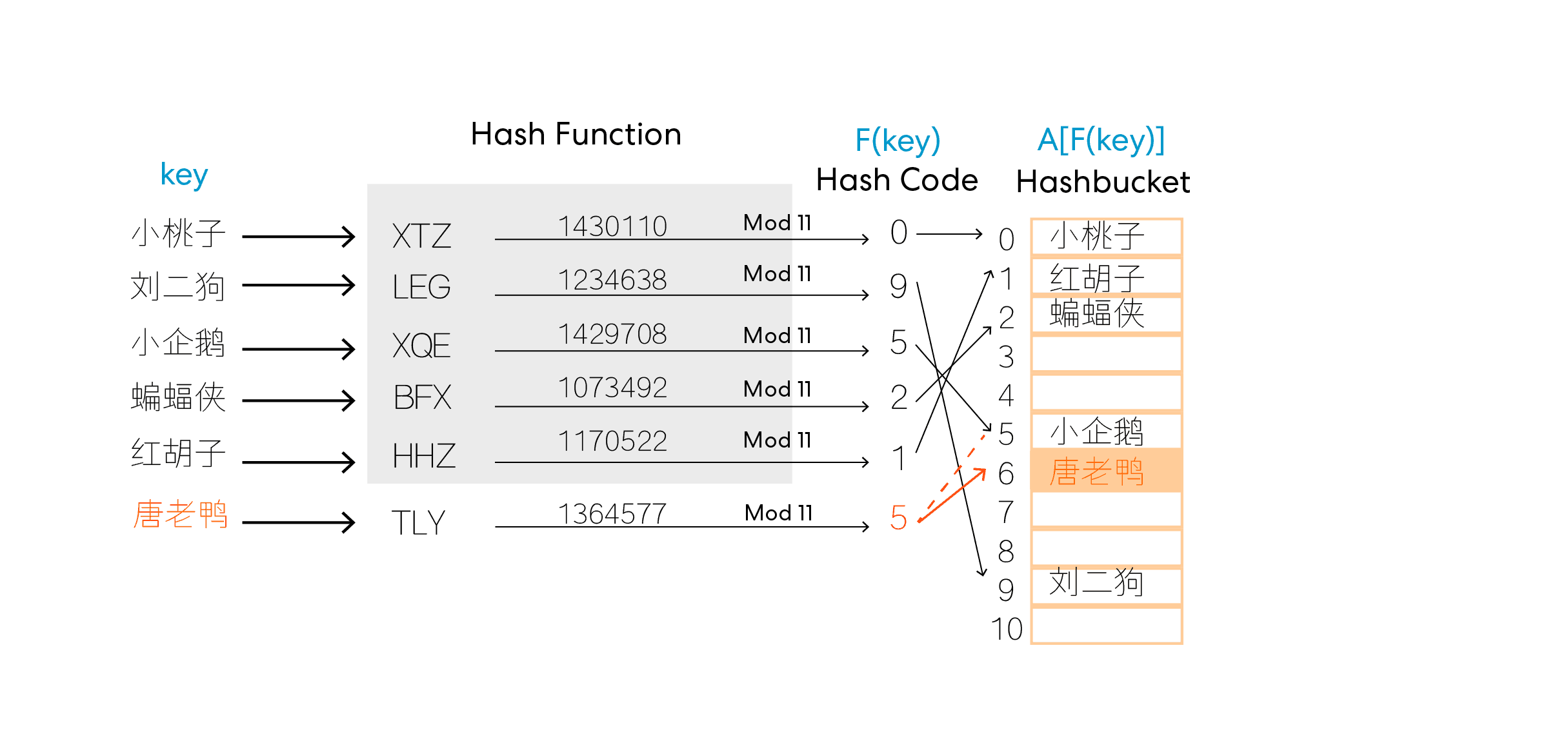
开放地址法的名字看上去很玄妙（哇，实在不知道open addressing还能翻译成什么），但是实际上就是：“如果这个抽屉有人占了就给你再换一个位置吧”。换位置的方法也有很多种，比较简（随）单（便）的方法就是直接放在隔壁下一个空抽屉里（线性探测 Linear Probing）。当然，直觉告诉我们这样过于简单以至于在hash表近乎满载（大部分抽屉都被占据）的时候查询效率大大降低（你就一直在隔壁的隔壁的隔壁的隔壁的抽屉里瞎找）。所以又有了Quadratic Probing（二次探测），也就是先找隔壁的，再一次就找隔4个，隔9个…以此类推，这样可以提速探测的过程（至少不用一个一个查了）。

当然，这样也不够理想，于是还有双哈希法（Double Hashing），比如说我们取key mod 7 作为第二个哈希函数，以返回值作为步长，然后在第一个哈希函数值冲突的时候继续加第二个值作为步长来找可用的索引值，其实现操作可以参考以下伪代码：

def double_hashing(hash_table, key, value): 
	index = hash_function1(key) 
	step_size = hash_function2(key) 
	start_index = index 
	while hash_table[index] is not None: 
		index = (index + step_size) % len(hash_table) 
		if index == start_index: 
			raise Exception("Hash table is full")
		hash_table[index] = (key, value)

不管采用哪种探测步骤，开放地址法的性能还是大大受哈希表负载程度：（负载程度 $Load Factor =\frac{Number of Elements}{Number of Buckets}$ ）影响的，一般来说这个系数需要维持在低于0.7，否则很可能导致长时间的探测。而且，在删除元素时也可能为后续的探测带来更大的复杂性（如果不特殊标记的情况下，无法知道此处时没有元素还是元素被删除，也影响后续是否继续探测）。尽管如此，开放地址法的内存的使用效率还是比链表法更高的，因为毕竟链表法还要存储指针（相当于是升了一维吧）。

综上所述，无论是依托于链表法还是开放地址法，哈希表的核心还是设计一个能使得数值尽可能均布的哈希函数来尽可能的减少哈希冲突。而链表法和开放地址法只能是补丁一般的存在，否则哈希表和普通的链表又有什么区别呢（严肃脸）。

实战练习：Leetcode 第一题！

Leetcode第一题就是典型的可以用hash表加速的题，

问题描述

Given an array of integers nums and an integer target, return indices of the two numbers such that they add up to target.

You may assume that each input would have exactly one solution, and you may not use the same element twice.

You can return the answer in any order.

Example 1: Input: nums = [2,7,11,15], target = 9 Output: [0,1]

Explanation: Because nums[0] + nums[1] == 9, we return [0, 1].

Example 2: Input: nums = [3,2,4], target = 6 Output: [1,2]

Example 3: Input: nums = [3,3], target = 6 Output: [0,1]

Constraints:

2 <= nums.length <= 10^4
-10^9 <= nums[i] <= 10^9
-10^9 <= target <= 10^9
Only one valid answer exists.

当然，最笨的办法就是采用双循环 $O(n^2)$ 暴力求和看是不是target然后返回。但我们很容易就想到做一个哈希表来加速。但是看到题目描述中，数据的量在正负10的9次方量级，暴力开数组当然会导致电脑爆炸啦。由于总共的元素不超过一万个，我又想要用双哈希的open addressing来解决冲突问题，所以稍微富裕一些取了一个两万五左右的大质数和两千左右的小质数来进行关键字映射。

class Solution(object):

	def twoSum(self, nums, target):
        hp1=25117
        hp2=1997    #预存两个质数

        def DoubleHash(a): #建哈希表的过程
            hash=[(None,-1)] *hp1 #开数组
            for i,x in enumerate(a): 
                code=x % hp1  #第一哈希函数映射地址
                if hash[code]==(None,-1):  #为空则填入
	                hash[code]=(x,i) 
                else: #不为空则按第二关键字查找
                    while hash[code]!=(None,-1): 
                        code=(code+((x % hp2)+1)) % hp1 #！此处取模后+1是细节啊，不然循环会卡住 别问我怎么知道的
                    hash[code]=(x,i) #再按照查到的空位填入
            return(hash)
            
        def searchhash(n): #哈希表查找函数
            code=n % hp1
            t,loc=self.h[code] #取出数值所在的地址和数值
            while (loc!=-1) and (t!=n): #若不为空 却不等于所查询的值 那么按照按照second hash继续查找
                code=(code+((n % hp2)+1)) % hp1 
                t,loc=self.h[code]
            if t==n: #若查询到所找的n，返回n所在位置，否则返回-1
                return(loc)
            else:
                return(-1)
		#主程序
        self.h=DoubleHash(nums) #建表 平均在O(n)
        for i,num in enumerate(nums): #查询 平均在O(n)
           result=searchhash(target-num)
           if (result!=-1) and (result!=i):
            return i,result

最后的运行时间的内存大小贴在下面，可以看到内存使用真的很大。感觉被只需要开一个数组的白痴办法吊打。不过相比较下面这张图里大约1996ms的运行时长的 $O(n^2)$ 重灾区，哈希表的大约40-50ms的运行时间是果然是根号级的优化。这大概用空间换时间吧（……。

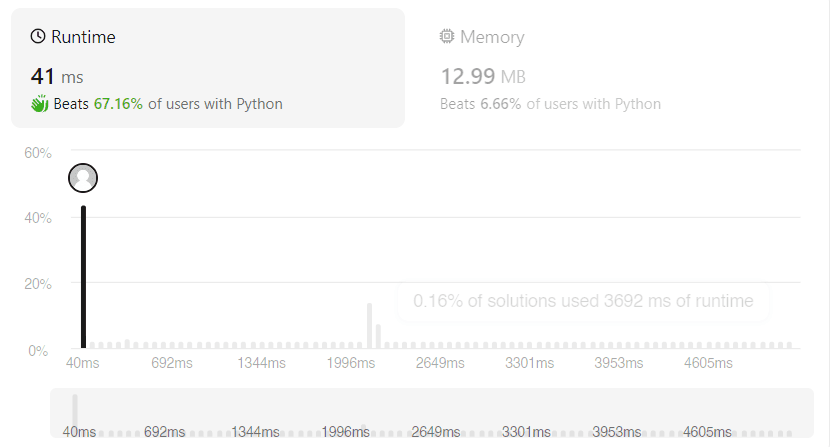
终于看到哈希表了。第一次接触哈希表大概十几年前吧，年少无知的时候不明白这玩意有什么用。现在感觉这东西在庞大的数据量的现在必须是个好东西。

-鹅仔 2024/5/12 19：29

属性